

Of course, to check whether a given vector b is in the range of T, you have to solve the matrix equation Ax = b to see whether it is consistent. To find a vector not in the range of T, choose a random nonzero vector b in R m you have to be extremely unlucky to choose a vector that is in the range of T. Whatever the case, the range of T is very small compared to the codomain. This means that range ( T )= Col ( A ) is a subspace of R m of dimension less than m : perhaps it is a line in the plane, or a line in 3-space, or a plane in 3-space, etc. Suppose that T ( x )= Ax is a matrix transformation that is not onto. The previous two examples illustrate the following observation.

Note that there exist tall matrices that are not one-to-one: for example,Įxample (A matrix transformation that is not onto)
This says that, for instance, R 3 is “too big” to admit a one-to-one linear transformation into R 2. Each row and each column can only contain one pivot, so in order for A to have a pivot in every column, it must have at least as many rows as columns: n ≤ m. The matrix associated to T has n columns and m rows. If T : R n → R m is a one-to-one matrix transformation, what can we say about the relative sizes of n and m ? Wide matrices do not have one-to-one transformations If you compute a nonzero vector v in the null space (by row reducing and finding the parametric form of the solution set of Ax = 0, for instance), then v and 0 both have the same output: T ( v )= Av = 0 = T ( 0 ).
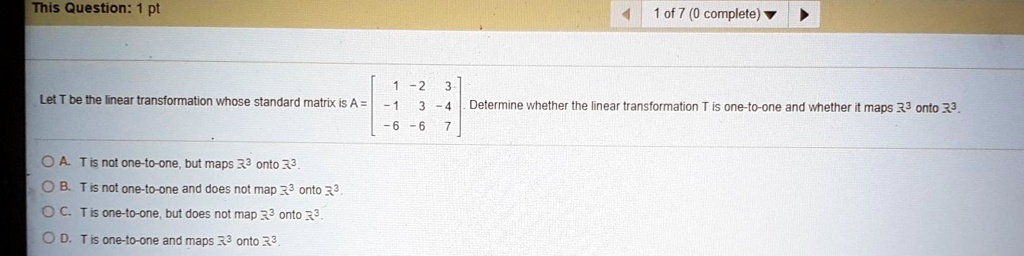
All of the vectors in the null space are solutions to T ( x )= 0. This means that the null space of A is not the zero space. By the theorem, there is a nontrivial solution of Ax = 0. Suppose that T ( x )= Ax is a matrix transformation that is not one-to-one. The previous three examples can be summarized as follows. Hints and Solutions to Selected ExercisesĮxample (A matrix transformation that is not one-to-one).3 Linear Transformations and Matrix Algebra


 0 kommentar(er)
0 kommentar(er)
